Solution Step1 Log 5 1000=Log(1000) ÷ Log(5) Log(1000)= 3 Log(5)= Log 5 1000=3 ÷ Ans= Step2 Alternatively, the logarithm can be calculated like this Log(500) Log(2)Symbolically, logn a = x For example, 10 3 = 1,000;Log(1000) = 3 l o g ( 1 0 0 0) = 3 ( ( ) )
Http Www Mellinamathclass Com Uploads 8 7 2 9 Unit 1c Lesson 5 5a Hw With Key Pdf
Log 1000=3
Log 1000=3-Ln (4x 1) = 3 ⇒ 4x – 3 =e 3In this article, all logarithms and exponents are to base 10, and decimal answers are rounded appropriately The logarithm of a number is the power to which 10 must be raised to equal that numberSome simple examples \(10^2 = 100\), therefore \(\log 100 = 2\)


2
Expressed in terms of common logarithms, this relationship is given by log mn = log m log n For example, 100 × 1,000 can be calculated by looking up the logarithms of 100 (2) and 1,000 (3), adding the logarithms together (5), and then finding its antilogarithm (100,000) in the tableFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepLog' 64 = 6 7) 6$ = 216 log# 216 = 3 8) 2Å% = log' = $4 Express each equation in exponential form 9) log& 32 = 5 2( = 32 10) log' 256 = 4 4) = 256 11) log( 125 = 3 5* = 125 12) log* 2 = 8 = 2 13) log 27 = 3 3* = 27 14) log' = ±3 4Å* = 15) log& = ±3 2Å* = 16) log, 1000 = 3 10* = 1000 2 1 16
Solve for x 3 log of x = log of 1000 Simplify by moving inside the logarithm For the equation to be equal, the argument of the logarithms on both sides of the equation must be equalIn this section we will introduce logarithm functions We give the basic properties and graphs of logarithm functions In addition, we discuss how to evaluate some basic logarithms including the use of the change of base formula We will also discuss the common logarithm, log(x), and the natural logarithm, ln(x)Similarly, log (1000) = 3, log (1/10) = –1, and so forth For all decibel calculations, use the common logarithm dB 10 log dB log log power reference power voltage current referencevoltage referencecurrent
1 Logarithmic Functions For any positive base b, where b ≠ 1or 0 and b > 0 b x = y if and only if x = log by Exponential Form Logarithmic Form 10 = log 1000 3 10 = Write in exponential formThe logarithm log b (x) = y is read as log base b of x is equals to y Please note that the base of log number b must be greater than 0 and must not be equal to 1 And the number (x) which we are calculating log base of (b) must be a positive real number For example log 2 of 8 is equal to 3 log 2 (8) = 3 (log base 2 of 8) The exponential is 2Sometimes we may see a logarithm written without a base In this case, we assume that the base is 10 In other words, the expression log (x) log (x) means log 10 (x) log 10 (x) We call a base10 logarithm a common logarithm Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section



Ale Find The Approximate Value Of Log10 1002 Given That Log10 E 0 4343 F X Log
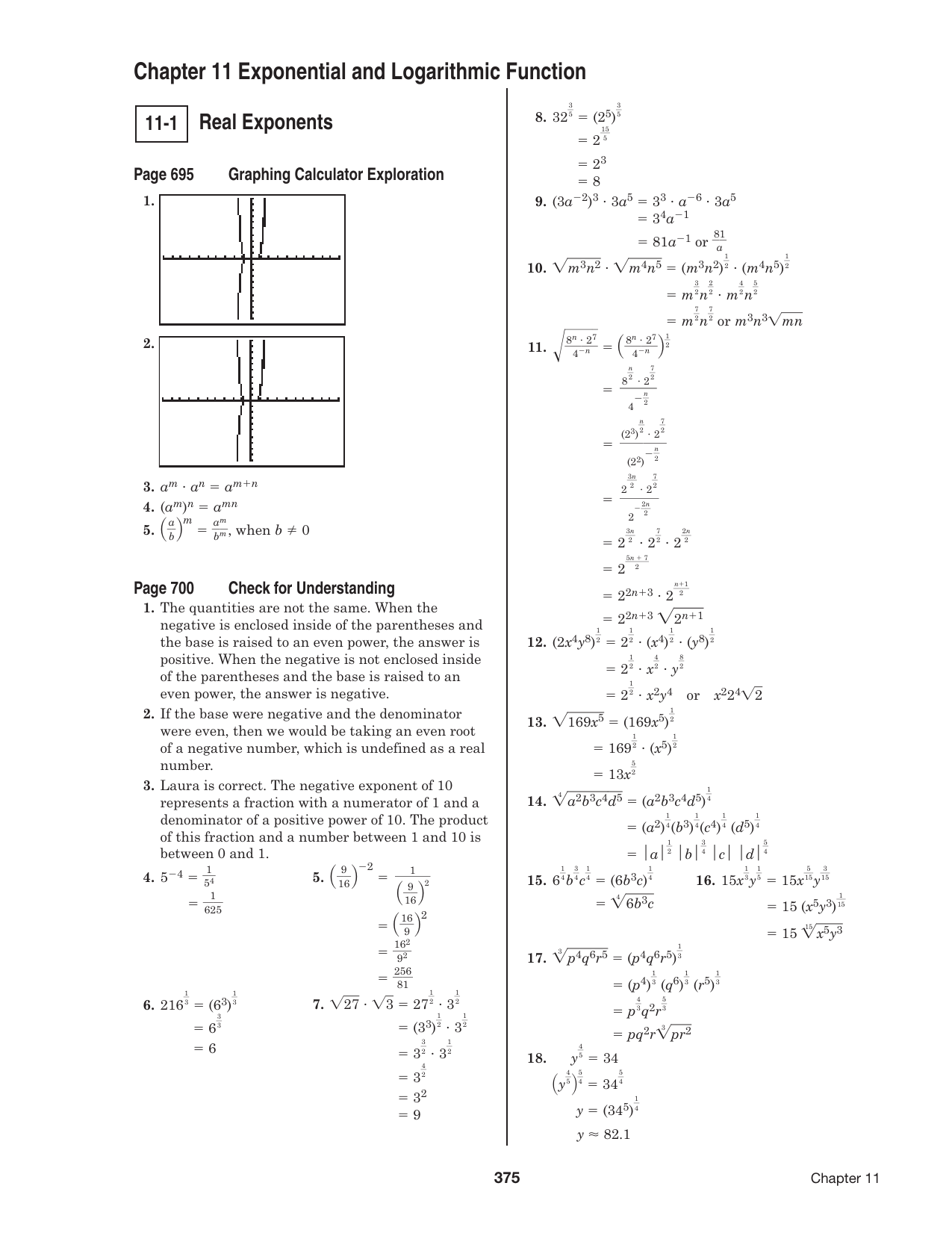


Chapter 11 Exponential And Logarithmic Function Manualzz
No changes made to narrative section of NPD 61 Associate Administrator 12/27/19 Chapter 5, 59 George C Marshall Space Center Update to organizational structure to include the Human Landing System Program Office No changes made to narrative section of NPDThe logarithm log b (x) = y is read as log base b of x is equals to y Please note that the base of log number b must be greater than 0 and must not be equal to 1 And the number (x) which we are calculating log base of (b) must be a positive real number For example log 2 of 8 is equal to 3 log 2 (8) = 3 (log base 2 of 8) The exponential is 2Then the log of x (base b) equals y log b (x)=y So, for example, using a base of 10 (log 10 or log base 10), the logarithm of 1,000 equals 3 because 10 raised to the three equals 1,000 If 10 raised to the power of three equals 1,000, 10 3 =1,000 then the log (base 10) of 1,000 equals 3 log 10 1000=3


Www Lmtsd Org Cms Lib Pa Centricity Domain 217 Pre calculus Hw scans Chapter 4 Pre calc 4 1 4 5 Pdf


Logarithms
Log 10 = 1, because 10 1 = 10;On dividing both sides by 2, we get;Therefore, log10 1,000 = 3



Antiderivative Of Log By Tutorcircle Team Issuu



Show That Log 1000 3 Log 2 3 Log 5 Brainly In
On a calculator it is the "log" button It is how many times we need to use 10 in a multiplication, to get our desired number Example log(1000) = log 10 (1000) = 3Chg# Approver Date Approved Description/Comments 77 Associate Administrator 10/27/ Chapter 5, 56 Lyndon B Johnson Space Center Updated organizational chart, no changes made to narrative section of NPD 76 Associate AdministratorMore generally, if latexx=b^y/latex, then latexy/latex is the logarithm base latexb/latex of latexx/latex, written latexy=\log_b(x)/latex, so latex\log_{10}(1000)=3/latex It is useful to think of logarithms as inverses of exponentials So, for example latex\displaystyle \log_b(b^z)=z/latex And



Solved 24 Determining Whether It Is True T Or False Chegg Com


Www Studocu Com En Ca Document High School Canada Advanced Functions Lecture Notes 5 Logarithmic Scales In The Physical Sciences View
Eg, since 1000 = 10 × 10 × 10 = 10 3, the "logarithm baseY = log b x if and only if b y = x for all x > 0 and 0 < b ≠ 1 Example 1 Write log 5 125 = 3 in exponential form 5 3 = 125 Example 2 Write log z w = t in exponential form z t = w{eq}\eqalign{ & {\text{In this particular case}}{\text{, we have the logarithmic expression}} \cr & \,\,\,\,\,\log 1000 = 3 \cr & \cr & {\text{Rewriting}} \cr
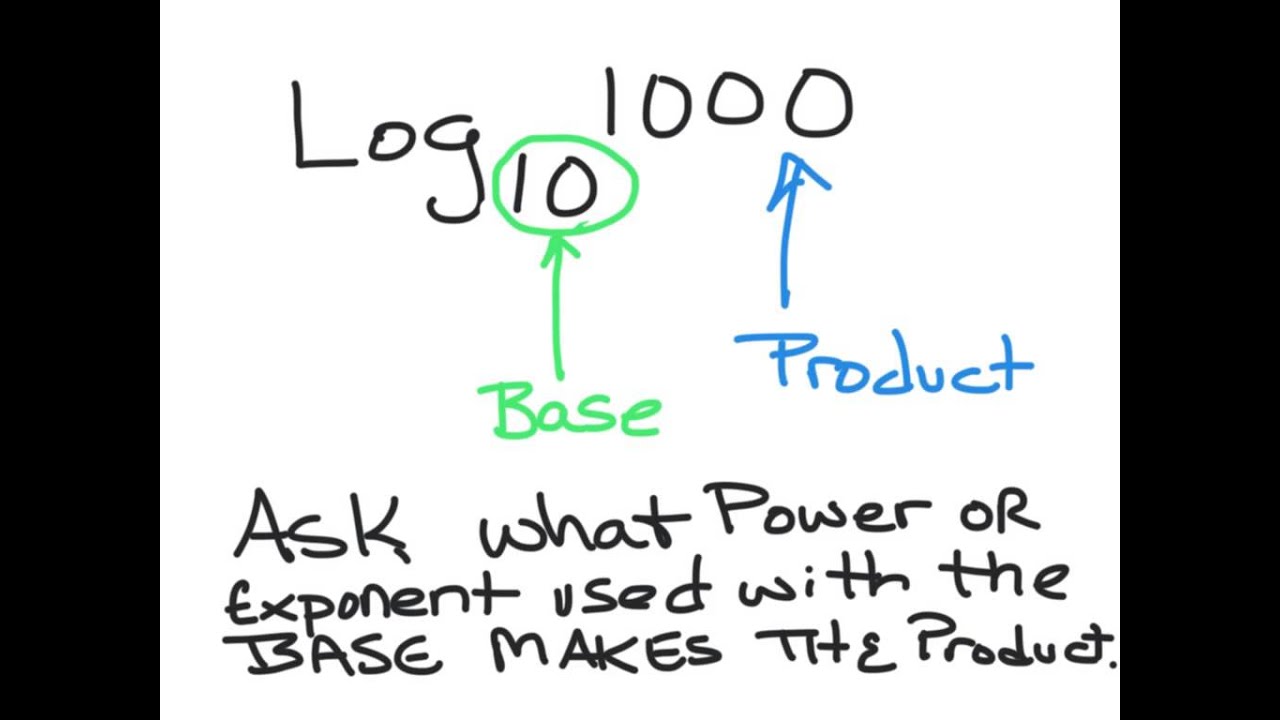


Log 10 1000 Youtube


1
Pinoybixorg is an engineering education website maintained and designed toward helping engineering students achieved their ultimate goal to become a fullpledged engineers very soonBack to top Bases and Arguments In a formula, the base is the subscript which you can find next to the letters logAccording to the rules of logarithm we know that log 1000= 3 As we by deafult have 10 in the base accordingly to the main rule We get 10³= 1000 Therefore, log x= 1 x^ 1 =10 1/x=10 X= 1/10 But accordin to calculus we have 'e' by deafult in the base
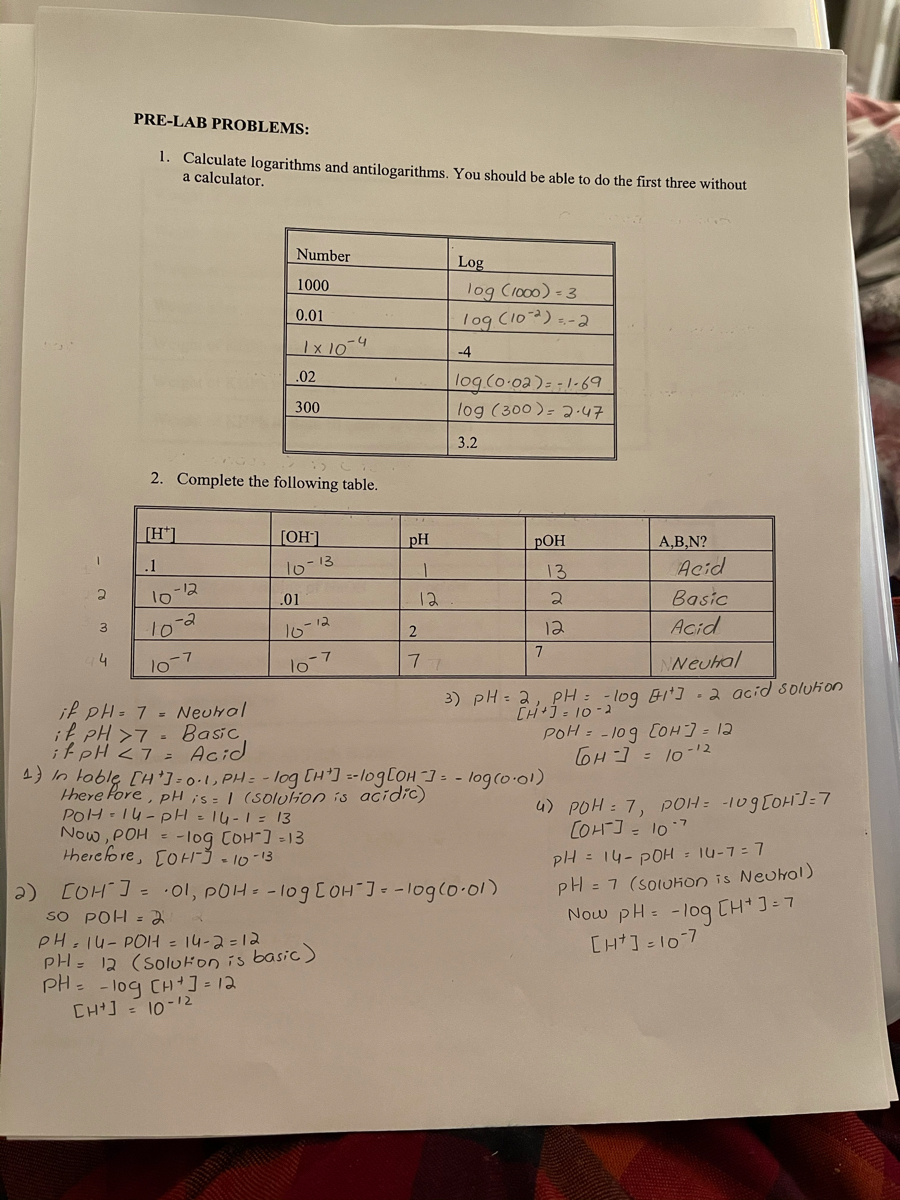


Answered Pre Lab Problems 1 Calculate Bartleby



Algebra 2 Unit 4 Interactive Notebooks Mastalio Math Mavericks
Log_10 1000=3 or simply log1000=3 This follows directly from the definition y=log_a x iff a^y=xThen the log of x (base b) equals y log b (x)=y So, for example, using a base of 10 (log 10 or log base 10), the logarithm of 1,000 equals 3 because 10 raised to the three equals 1,000 If 10 raised to the power of three equals 1,000, 10 3 =1,000 then the log (base 10) of 1,000 equals 3 log 10 1000=3See Logarithm rules Logarithm product rule The logarithm of the multiplication of x and y is the sum of logarithm of x and logarithm of y log b (x ∙ y) = log b (x) log b (y) For example log 10 (3 ∙ 7) = log 10 (3) log 10 (7) Logarithm quotient rule


Q Tbn And9gcqqbcxeqtlqebpatbmasqpnicdupbrpft 5eb2ypnrn0wrtwrjp Usqp Cau


Www Tsfx Edu Au Free Vce Hsc Resources 18 02 N3 7 Logarithmicfunctions Pdf
Log 10 (2x 1) = 3 After writing it in exponential form we get 2x 1 = 10 3 2x 1 = 1000 2x = 999 x = 4995 Check x = 4995 log10 (2 x 4995 1) = log10 (1000) = 3 since 103 = 1000 Sometimes when you solve logarithmic equations, you need to put all the logarithms on one side of the equation10 3 = 1000 ดังนั้น log 10 1000 = 3;Solution for log(1000)=3 equation Simplifyinglog(1000) = 3Reorder the terms for easier multiplication1000glo = 3Solving1000glo = 3Solving for variable 'g' Move all terms containing g to the left, all other terms to the right Divide each side by '1000lo'g = 0003l1o1Simplifyingg = 0003l1o1


2



Ss1 Mathematics 1st Term Lesson Notes Evaluation Tests Page 7 Of 8 Ssce Waec Neco Preparatory Portal For Ss1 Ss2 And Ss3
If we raise 10 to the power of 3, we get 1000 10 3 = 10 x 10 x 10 = 1000 The logarithm function is the reverse of exponentiation and the logarithm of a number (or log for short) is the number a base must be raised to, to get that number So log 10 1000 = 3 because 10 must be raised to the power of 3 to get 1000Latex{\mathrm{log}}_{}(1000)=3/latex Example Evaluate latexy={\mathrm{log}}_{}(321)/latex to four decimal places using a calculator Show Solution, ) In our last example, we will use a logarithm to find the difference in magnitude of two different earthquakes Example The amount of energy released from one earthquake was latexThe logarithm is defined as the inverse of the exponential Since 104= 10,000, it follows by definition that log 10,000 = 4 Similarly, log 1,000 = 3 and log 1,000,000 = 6 Note that logs can be defined with respect to bases other than 10, but here we will restrict ourselves to logs to the base 10


2
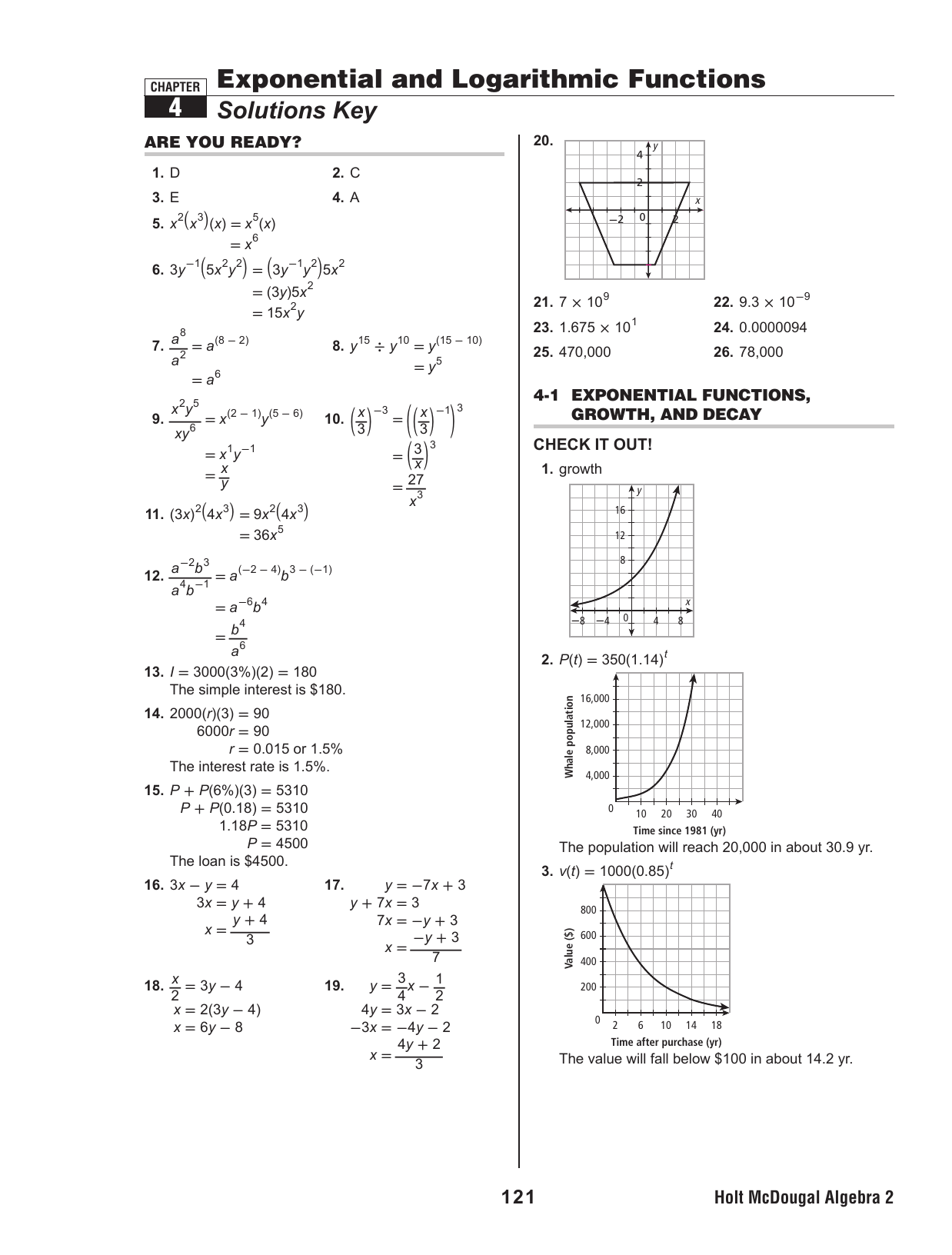


Exponential And Logarithmic Functions 4 Manualzz
2 5 = 32 ดังนั้น log 2 32 = 5;What is the value of log to base 10 of 1000^33?X = 4995 Verify your answer by substituting it in the original logarithmic equation;


Http Www Mellinamathclass Com Uploads 8 7 2 9 Unit 1c Lesson 5 5a Hw With Key Pdf


Www Cusd80 Com Cms Lib Az Centricity Domain 972 Notes 15 1 key Pdf
Symbolically, logn a = x For example, 10 3 = 1,000;We saw above that base ten logarithms are expressions in which the number being raised to a power is ten The base ten log of 1000 is three log 1000 = 3 103= 1000 So far, we've worked with expressions that have whole numbers as solutionsTherefore, since Log 10 (1000)= 3, the antilog 10 of 3 is 1,000 Taking the antilog of X raises the base of the logarithm in question to X


People Engr Ncsu Edu Mbs Books Microwaverfdesign Rf First Edition Appendix b Appendix b additional examples Pdf


2
Log 1000 = 3, because 10 3 = 1000;⇒ log 10 (2 x 4995 1) = log 10 (1000) = 3 since 10 3 = 1000 Example 4 Evaluate ln (4x 1) = 3 Solution Rewrite the equation in exponential form as;This free log calculator solves for the unknown portions of a logarithmic expression using base e, 2, 10, or any other desired base Learn more about log rules, or explore hundreds of other calculators addressing topics such as math, finance, health, and fitness, among others



Answered Use The Definition Of The Logarithmic Bartleby



22 And 23 Question Lt Br Gt If Log3 0 477 And 1000 Is To The Power X 3 Then X Equals Brainly In
Simplifying log (x) * 1000 = 3 Reorder the terms for easier multiplication 1000glo * x = 3 Multiply glo * x 1000glox = 3 Solving 1000glox = 3 Solving for variable 'g' Move all terms containing g to the left, all other terms to the right Divide each side by '1000lox' g = 0003l 1 o 1 x 1 Simplifying g = 0003l 1 o 1 x 1Log Base 10 Log base 10, also known as the common logarithm or decadic logarithm, is the logarithm to the base 10 The common logarithm of x is the power to which the number 10 must be raised to obtain the value x For example, the common logarithm of 10 is 1, the common logarithm of 100 is 2 and the common logarithm of 1000 is 3Similarly, log (1000) = 3, log (1/10) = –1, and so forth For all decibel calculations, use the common logarithm dB 10 log dB log log power reference power voltage current referencevoltage referencecurrent
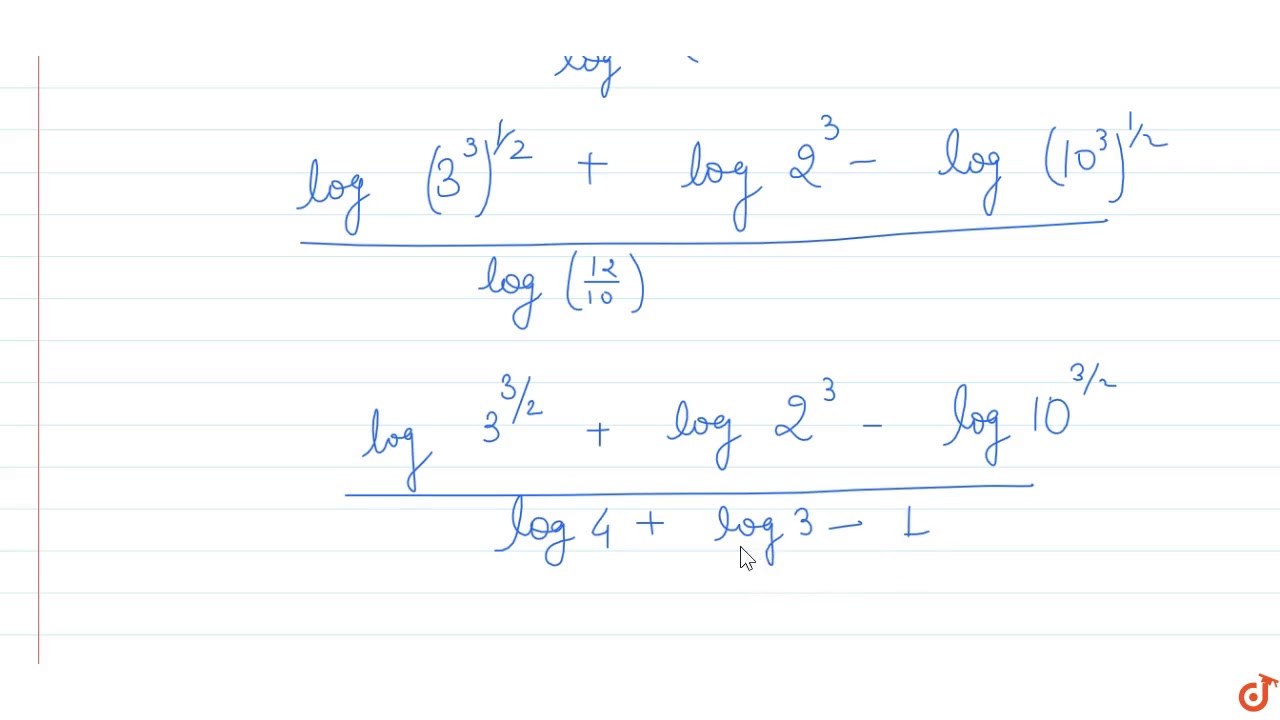


Log Sqrt 27 Log8 Log Sqrt 1000 Log 1 2 Find The Value Youtube



Common Logarithms Ppt Download
1 Logarithmic Functions For any positive base b, where b ≠ 1or 0 and b > 0 b x = y if and only if x = log by Exponential Form Logarithmic Form 10 = log 1000 3 10 = Write in exponential formHow do you solve #log _(x2) 1000 = 3#?What is the value of log to base 10 of 1000^33?


Www Humbleisd Net Cms Lib2 Tx Centricity Moduleinstance Ch 7 3 Reteach Pdf



Logarithmic Functions Ppt Download
In mathematics, the logarithm is the inverse function to exponentiationThat means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number xIn the simplest case, the logarithm counts the number of occurrences of the same factor in repeated multiplication;Logarithms Explained If you are familiar with the exponential function then you should know that its logarithmic equivalence is These two seemingly different equations are in fact the same or equivalent in every way Look at their relationship using the definition below Definition of a Logarithmic Function The purpose of the equivalent equations, as Logarithms Explained Read More »Log 1000 = 3 log 101 = which appears has been rounded to you're told to take (63) and divide it by to get 694 (63) = 3, so the equation becomes 3/ = 694 I do it on my calculator and i get that rounds to 694, so i'm at least in the right direction



Lesson Video Evaluating Logarithms



2 3
Log 100 = 2, because 10 2 = 100;1000 3 4 Instead, you can use the logarithm rule with log tables and get a relatively good approximation of the result If you had a log table, you could quickly check the logarithm of these numbers (or you use the Internet to find an electronically uploaded table),Therefore, log10 1,000 = 3
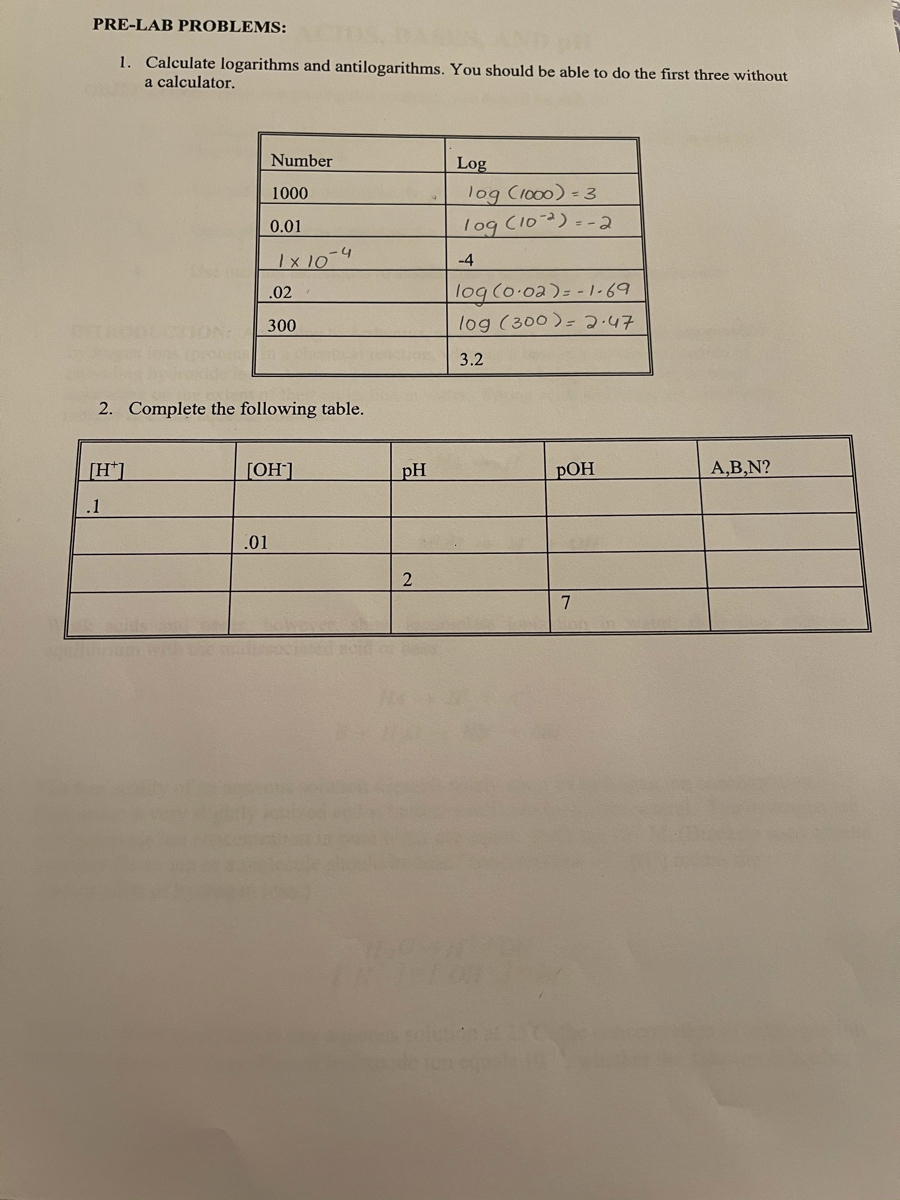


Answered Pre Lab Problems 1 Calculate Bartleby


Cnx Org Exports 746b4be7 5dfd 4d01 93 06ef750e0365 3 Pdf Logarithmic Functions 3 Pdf
Precalculus Solving Exponential and Logarithmic Equations Logarithmic Models 1 AnswerM = log 10 A B 其中: A 是地震仪测量的振幅(单位为毫米) B 是距离校正系数 现今有更复杂的公式,但都是用对数尺度。 声音 响度的单位是分贝(简写为dB): 响度(dB) = 10 log 10 (p × 10 12) 其中 p 是声压 酸性的或碱性的 酸性(或碱性)的测量单位是 pH: pHLog 1000 = 3 log 101 = which appears has been rounded to you're told to take (63) and divide it by to get 694 (63) = 3, so the equation becomes 3/ = 694 I do it on my calculator and i get that rounds to 694, so i'm at least in the right direction


2


Www Alvinisd Net Cms Lib Tx Centricity Domain 436 Dc college algebra chapter 6 review solutions Pdf
Log (1000/2), 1000/2 equals 500, they are still the same to the initial question since log 1000=3, and as per the question, where log 2 is given as , and considering the law of logarithm where log (a/b) is equal to loga log b, the question can be simplified as log 1000log 2 which is (3–) the answer is therefore 2699Logarithms Explained If you are familiar with the exponential function then you should know that its logarithmic equivalence is These two seemingly different equations are in fact the same or equivalent in every way Look at their relationship using the definition below Definition of a Logarithmic Function The purpose of the equivalent equations, as Logarithms Explained Read More »Sometimes we may see a logarithm written without a base In this case, we assume that the base is 10 In other words, the expression log (x) log (x) means log 10 (x) log 10 (x) We call a base10 logarithm a common logarithm Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section


Cdn Fs Teachablecdn Com 9rvowasctoiw1ginjigv


2
1000 3 4 Instead, you can use the logarithm rule with log tables and get a relatively good approximation of the result If you had a log table, you could quickly check the logarithm of these numbers (or you use the Internet to find an electronically uploaded table),Log·a·rithm (lô′gərĭth′əm, lŏg′ə) n Mathematics The power to which a base, such as 10, must be raised to produce a given number If nx = a, the logarithm of a, with n as the base, is x;Take into consideration the following property If log of (a) base (b) = c, then b^c = a Here, log base x of 1000 =3 So, x^3 = 1000


2


2
More generally, if latexx=b^y/latex, then latexy/latex is the logarithm base latexb/latex of latexx/latex, written latexy=\log_b(x)/latex, so latex\log_{10}(1000)=3/latex It is useful to think of logarithms as inverses of exponentials So, for example latex\displaystyle \log_b(b^z)=z/latex Andลอการิทึมของ x ในฐาน b เขียนแทนด้วย log b x หรือถ้าฐานมีค่าใด ๆ เป็นปริยาย จะเขียนเพียงแค่ log xLog 10,000 = 4, because 10 3 = 10,000;



2 Example 3 Example


Http Www Kingscollege Net Camiletti 12 T5 2 Pdf
Pinoybixorg is an engineering education website maintained and designed toward helping engineering students achieved their ultimate goal to become a fullpledged engineers very soonIn this section we will introduce logarithm functions We give the basic properties and graphs of logarithm functions In addition, we discuss how to evaluate some basic logarithms including the use of the change of base formula We will also discuss the common logarithm, log(x), and the natural logarithm, ln(x)M = log 10 A B 其中: A 是地震仪测量的振幅(单位为毫米) B 是距离校正系数 现今有更复杂的公式,但都是用对数尺度。 声音 响度的单位是分贝(简写为dB): 响度(dB) = 10 log 10 (p × 10 12) 其中 p 是声压 酸性的或碱性的 酸性(或碱性)的测量单位是 pH: pH



1 Exponential To And Logarithmic Expressions


2
Explanation Using law of logarithms Reminder ∣∣ ∣ ∣¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯a a logbx = n ⇔ x = bn a a ∣∣ −−−−−−−−−−−−−−−−−−−−−− Relating to the given question x = 1000 , b = x and n = 3 ⇒ 1000 = x3 ⇒ 103 = x3 ⇒ x = 10 Answer linkLog·a·rithm (lô′gərĭth′əm, lŏg′ə) n Mathematics The power to which a base, such as 10, must be raised to produce a given number If nx = a, the logarithm of a, with n as the base, is x;Log (100,000) = 5, log (10,000) = 4, log (1,000) = 3, log (10) = 1 The exception and special case is log x (0) = Undefined That is so because there is no power to which you can raise any number and obtain 0 (zero) You can asymptotically approach zero, but you cannot get to zero



Log De 1000 Na Base X 3 Brainly Com Br


2
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe logarithm is defined as the inverse of the exponential Since 10 4 = 10,000, it follows by definition that log 10,000 = 4 Similarly, log 1,000 = 3 and log 1,000,000 = 6 Note that logs can be defined with respect to bases other than 10, but here we will restrict ourselves to logs to the base 10 Logs can also be negative10 = 1 10) = 100 so, log 100 = 2 10 " = 1000 so, log 1000 = 3 CC BY Andrew Binham Input Output /(1) = 2 3 / 4(1) = log) 1 1 = 3 3 2 " = 8 1


Http Www Astro Indiana Edu Darkuniverse Logarithms Pdf



Ejercicios De Logaritmos Docsity
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more1000 3 4 Instead, you can use the logarithm rule with log tables and get a relatively good approximation of the result If you had a log table, you could quickly check the logarithm of these numbers (or you use the Internet to find an electronically uploaded table),


Oakbay Public Sd61 Ca Wp Content Uploads Sites 37 13 06 Math 12 Logs Answers Pdf


Http Www Webassign Net Question Assets Stitzca1 6 3 Pdf



Solved 2 Fit To Page I Page View Av Read Aloud 1 Add No Chegg Com



Logarithms Ppt Video Online Download



2 33 Log 33 5 3 729 Log 729 3 5 5 Log 5 1 16 Log 16 4 7 1 Log 1 0 5 Log Logarithm Exponentiation



Ppt 11 5 Common Logs And Natural Logs Powerpoint Presentation Free Download Id


Services Artofproblemsolving Com Download Php Id Yxr0ywnobwvudhmvocl2zkyjrhyza4nzmxy2m3mda4zwezogvmyjiwyzg5mda0zwvlzdji Rn Yxjtbhrlyw0ymdewlnbkzg


2



Investigate 6 2 Mjns



Base 10 Logarithm Logarithmic Properties Logarithmic Form Exponential Form Of Logarithmic Function Logarithmic Scale Logarithmic Functions Equations Math


Http Www Donrmath Net M119 Unit4 Lesson4 Mathcad u4l4 Pdf



4log2 4 16 Log2 3 125 Log 125 5 Log


2



Proof Of The Logarithm Product Rule Video Khan Academy



Q 22 If Log 3 0 477 And 1000 Xx 3 Then X Equals A 0 0159



Ppt 5 4 Common And Natural Logarithmic Functions Powerpoint Presentation Id


2


Http Quantum Bu Edu Courses Ch102 Spring 16 Notes Logarithmstutorial Abridged Pdf



Basic Math Logarithms Env710 Statistics Review Website


2



Logarithms Ppt Video Online Download



Express Each Of The Followi Log 1000 3evaluate The Following I


Www Cusd80 Com Cms Lib Az Centricity Domain 972 Notes 15 1 key Pdf


2


Www Cbsd Org Cms Lib Pa Centricity Domain 40 3 2 log functions hpc notes Pdf


Http Www Dvusd Org Cms Lib07 Az Centricity Domain 2669 8 4 solving log eq Pdf


2


2


Jmsmathzone Weebly Com Uploads 3 8 2 1 Logarithms Extra Practice Pdf



Log Exp Form Num1 Mathematical Objects Complex Analysis



Solution What Is The Value Of Log To Base 10 Of 1000 3 3


2


2


Www Jstor Org Stable



Logarithm Part 1 Introduction Youtube


Http Faculty Montgomerycollege Edu Fkatira1 Math115anotesforsection33solutions Pdf



4 3 Cp43 Handout



Ppt Prerequisites For Chem 101 Powerpoint Presentation Free Download Id



Anti Derivative Of Log Logarithm Integral


Www Selfstudys Com Get Pdf


Www Lcps Org Cms Lib Va Centricity Domain Unit 6 day 3 log properties jw 19 completed b6 Pdf



Section 1 Logarithms Pdf Free Download



Logarithms And Fast Calculations Jeremy Renfro Pdf Free Download


Q Tbn And9gcrezvsfyzfngextetf3itn5tiwf2ps6ccekd26plpswiz7gmuzv Usqp Cau


2


2



Show That Log8 1000 Is Equal To Log2 10 Change Base T5 Youtube


Oakbay Public Sd61 Ca Wp Content Uploads Sites 37 13 06 Math 12 Logs Answers Pdf


2



Logarithm Docx Logarithm Exponentiation



Chapter Five Solutions For Section 5 1 Skill Refresher Exercises Pdf Free Download


Www Lmtsd Org Cms Lib Pa Centricity Domain 172 7 4 notes Pdf


Portal Sd22 Ca Class T9atw3l Lists Handoutsandmaterials Chapter 08 Pc12 08 1 Notes Pdf


Rankin Instructure Com Courses Files Download Download Frd 1


2



Log 27 Log8 Log 1000 Log 1 3 2 Brainly In


Relation Between Exponential And Logrithmic Functions Video Dailymotion



0 件のコメント:
コメントを投稿