円 内接 三角形 角度 305728-円 内接 三角形 角度

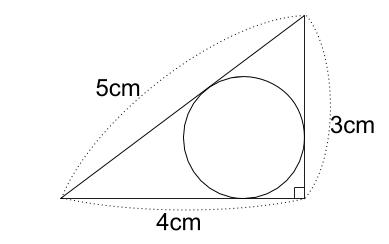
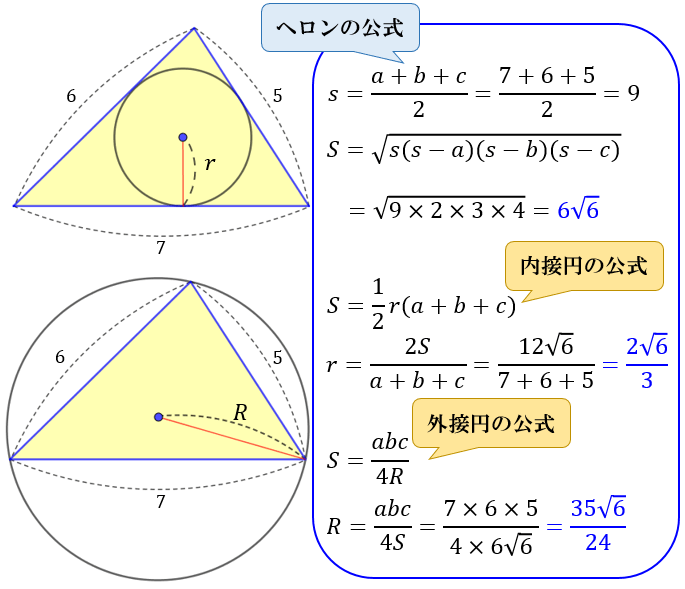
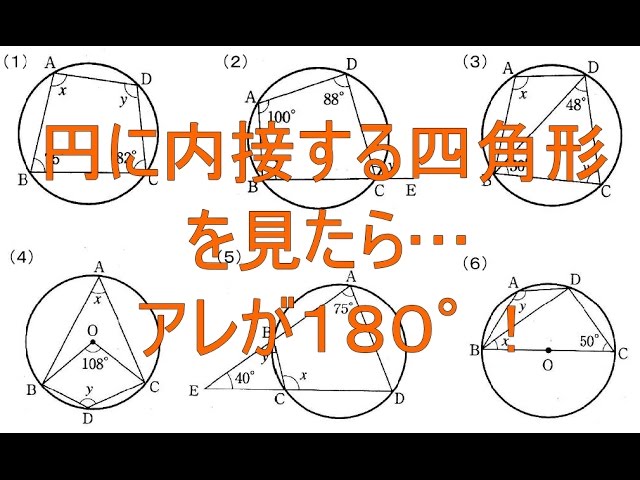
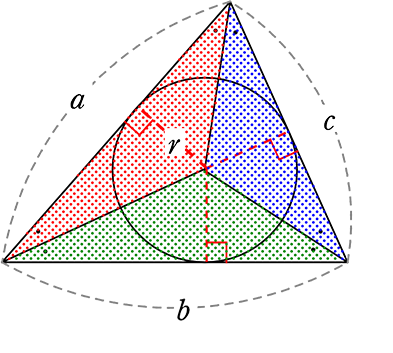
外接円、内接円などは三角比とともに融合されてよく出てきますが、1つひとつ確認していきましょう。 例題1では角度についてです。 これは中学生でも知っている人は多いでしょう。 「 円に内接する四角形の内対角の和は180° 」 ･･･①以下の直角三角形を考えます。 この直角三角形に内接する円を描きます。 円の半径は\(r\)であるとします。 この\(r\)を三角形の各辺の長さ\(a,b,c\)で表現する方法を考えましょう。 それには、まず下の図の⇔で示した直線の長さに注目します。第50問 内接円と外接円 図形ドリル 5年生 6年生 内接円 円 外接円 正方形 ★★★☆☆☆ （中学入試標準レベル） 思わず「お～～！！」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは，色々なタイプの図形問題を

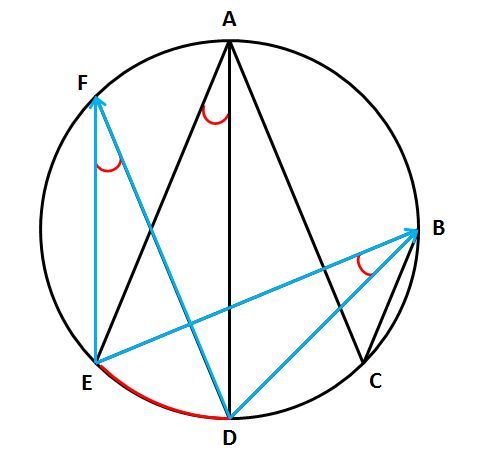
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

円 内接 三角形 角度

円 内接 三角形 角度-円について角度の問題を解いてみましょう。はじめに基礎知識を確認します。図1： 同じ弧に対する円周角は等しい。 （円周角の定理）図2： 円周角＝中心角／2 （円周角の定理） ・・＋・・＝2（・＋・） となっている。 図3： 半円の円周角＝こんにちは。 da Vinch (@mathsouko_vinch)です。 正弦定理と外接円正弦定理を紹介した時に外接円については触れなかったので、ここで少し確認したいと思います。まず「外接円」とは何かというと三角形の3つの頂点全てを通る

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

方べきの定理は、実生活では等式そのものよりも「円と直線の交点 \(a,b,c,d,p,x\) によって作られる2組の三角形がそれぞれ相似である」ということが重要な定理です。 「どの三角形とどの三角形が相似なのか？円や角度に関する作図はこちらもご参考ください(^^) 円の中心を作図する方法とは？ 難問円に内接する正三角形の作図方法とは？ 角度15°・30°・45°・60°・75°・90°・105°の作り方とは？円に内接している三角形の面積の求め方について教えてほしいです。円に内接している三角形をABCとおき、円の中心OからBCに垂線をおろし、その交点をH、距離をt、そして半径をrとする。このとき、三角形の面積は1/ 数学 解決済 教えて！goo

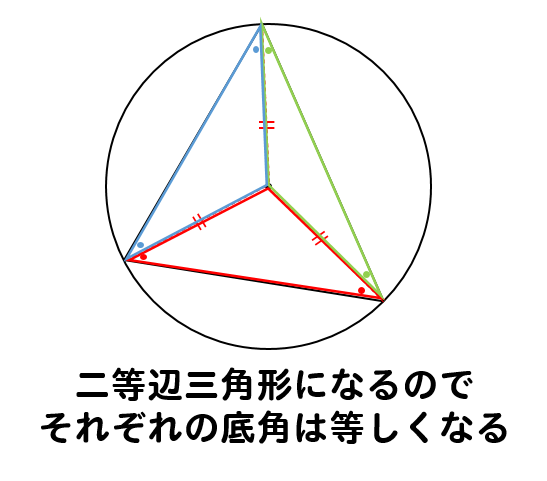
性質 任意の円は、任意の三つの角度を持つ三角形（もちろん角度の和は 180° に等しい）を内接三角形として持つ。 任意の三角形は適当な円に内接する（そのような円は、その三角形の外接円と呼ばれる）。;（解答） OCA は，二等辺三角形だから2つの底角は等しい．（右図の緑で示した角 x ） 同様にして， OAB も二等辺三角形だから2つの底角は等しい．（右図の黄色で示した角 37° ） 次に，円周角は中心角の半分だから ∠ x=18° （答）以下の直角三角形を考えます。 この直角三角形に内接する円を描きます。 円の半径は\(r\)であるとします。 この\(r\)を三角形の各辺の長さ\(a,b,c\)で表現する方法を考えましょう。 それには、まず下の図の⇔で示した直線の長さに注目します。

下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば三角形には不思議な性質がたくさんあります。 その中にはまだ発見されていないものもあるはずです。 このジオジェブラを使うと正確な作図が簡単にでき、さらにアニメーションを使って変化を調べることができ、新しい発見が容易にできます。 「bもしかしたら・・・？円について角度の問題を解いてみましょう。はじめに基礎知識を確認します。図1： 同じ弧に対する円周角は等しい。 （円周角の定理）図2： 円周角＝中心角／2 （円周角の定理） ・・＋・・＝2（・＋・） となっている。 図3： 半円の円周角＝

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

正方形の一辺を2とすると 内接円の半径が1 外接円の半径が√2 なので、 外接円の一点(a)と内接円の中心(b)と内接円の直径との交点(c)で できる三角形abcは、 ab=√2 bc=1 ゆえに tan(θ)=1/√2≒ のθを求めて、その角度を倍すればいいと思うのですが。三角形の内心 、三角形の内接円 この1点で交わった点 i を三角形の内心という。 内心 i を中心として、 半径 il の円が三角形の内接円である。 il＝im＝in il⊥bc 、 im⊥ac 、 in⊥ab第162問 円に内接する図形 図形ドリル 6年生 二等辺三角形 正五角形 正方形 角度 ★★★★☆☆（中学入試難関校レベル） 思わず「お～～！！」と言いそうな良問を。受験算数の定番からマニアックな問題まで。

内接円 内心

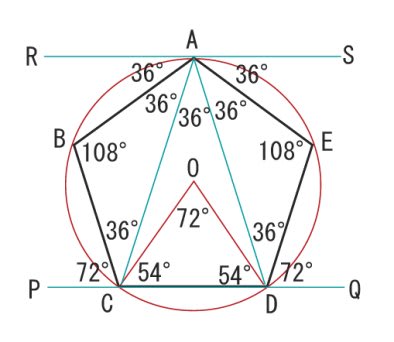
正五角形というだけで 分かる角度は 名寄 算数数学教室より

円の特徴 ここでは、同じ弦をもつ三角形に外接している円の特徴について説明しましょう。 図のように円の中に ABP、 AQB、 ABRがあるとします。 この三角形はABを共通の底辺としてもっていますね。 このような状況にあるとき、∠APB＝∠AQ円の特徴 ここでは、同じ弦をもつ三角形に外接している円の特徴について説明しましょう。 図のように円の中に ABP、 AQB、 ABRがあるとします。 この三角形はABを共通の底辺としてもっていますね。 このような状況にあるとき、∠APB＝∠AQ正三角形を作ることができる というわけですね。 作図手順の解説 それでは、まず円を6等分していきましょう！ そのためには、円の中心を求める必要があるので 円の中心を作図してやります。 円の中心は、円周上のどの点からも等しい距離にある点です。

円の中にある二つある三角形の角度の求め方 数学 解決済 教えて Goo

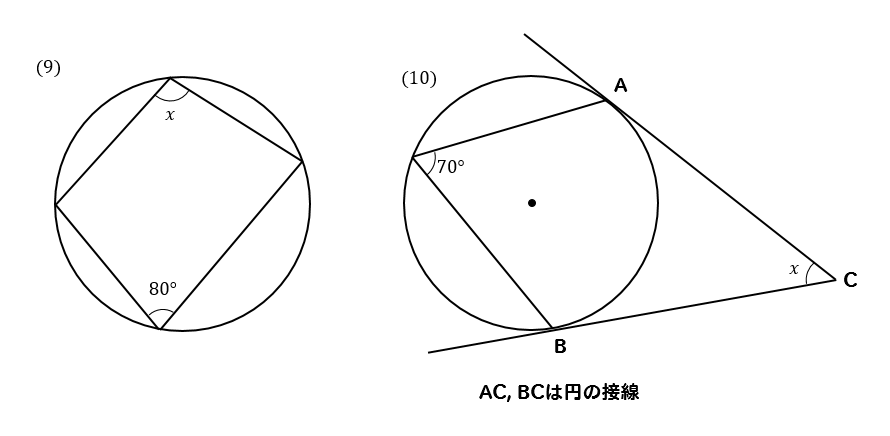
これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ

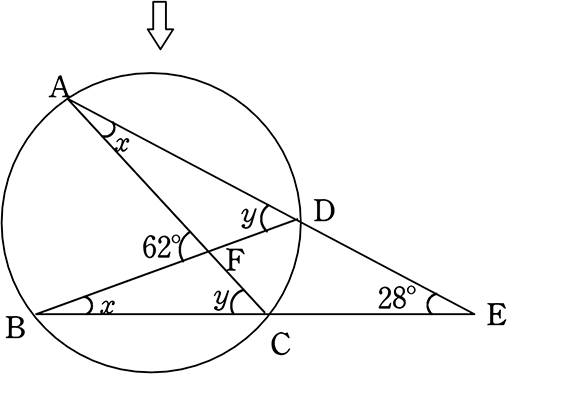
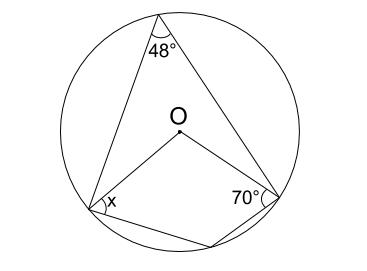
中心の上に立つ円周角は90°だから，上側の三角形は直角三角形 その直角三角形で右側の角は70°になる 円に内接する四角形で，70°と向かい合う内角が求める∠dだから∠d70°=180° → ∠d=110°円や角度に関する作図はこちらもご参考ください(^^) 円の中心を作図する方法とは？ 難問円に内接する正三角形の作図方法とは？ 角度15°・30°・45°・60°・75°・90°・105°の作り方とは？角度 を求める問題 a→fとする。四角形dbfcは円に内接し、 fbd、 fadは二等辺三角形。 DC上に∠CBF＝40となるFをとる。正三角形EBF、 EAFは底角10の二等辺三角形でDAEFは円に内接する。

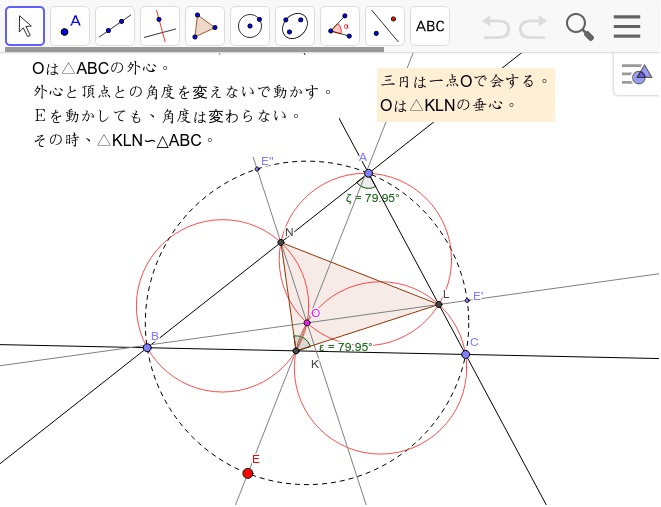
三角形に内接する相似三角形 Geogebra

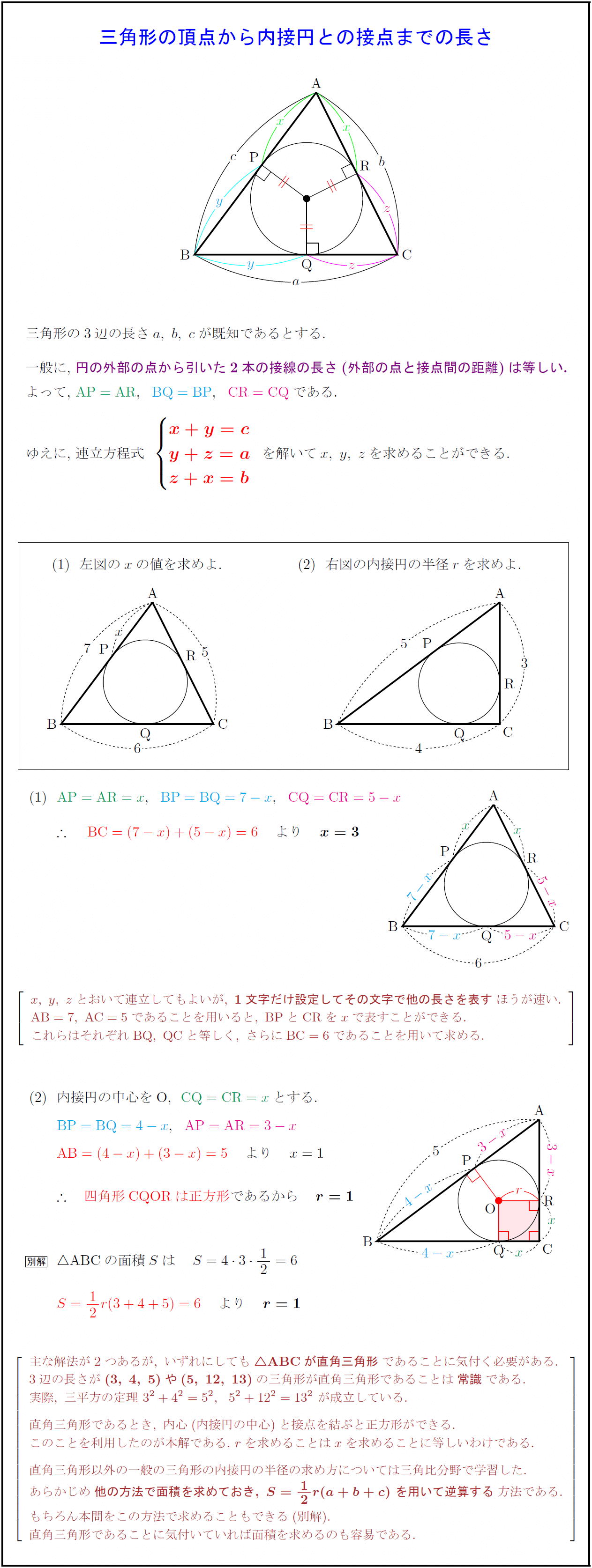
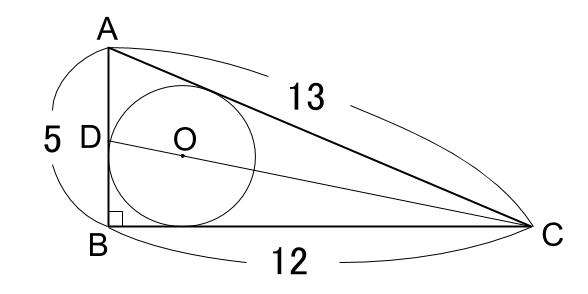
高校数学a 三角形の頂点から内接円との接点までの長さ 受験の月

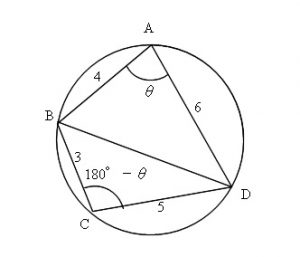
三角形であれば頂点が3つあれば良いので、 このように球面上の三角形（球面三角形）を作る事が出来ます。 ② 斜辺10cm、高さ6cmの「球面直角三角形」 球面三角形のある頂点の角度は、その頂点を通る2つの断面円（平面）が成す角度です。円に内接する四角形の性質 1：円に内接する四角形の対角の和は180° 2：四角形の内角は、その対角の外角に等しい このテキストでは、これらの定理を証明します。 「円に内接する四角形の対角の和は180°」の証明 四角形ABC角度を求めて下さい。 図のように、円に内接する五角形abcdeがあり、点fは辺bcの延長上にある。∠cab=50゜∠bca=37゜、ab=cdのとき、次の角の大きさを求めよ。 (1)∠cda (2

円による角度の求め方 中学数学に関する質問 勉強質問サイト

中学数学 円周角 中心角

三角形の内接円の半径の利用 ・ 頂点の角度と円周の関係 ・ 内接円を持つ四角形の対辺の関係 イ 円周角と中心角の関係の活用 ① 接弦定理 ・ 接弦定理の証明 ・ 接弦定理の逆 ② 方べき ・ 方べきの定理の証明 ③ 方べきの定理の逆 ・ 方べきの定理の①円に内接する四角形の性質 どんな三角形にも外接円と内接円は存在するが、四角形には必ずしも存在するとは限らない。 まず円に内接する四角形の性質を考える。円に内接する好きな四角形をいくつか書いて、 それぞれの四角形の4辺の長さと4つの角度三角形の内心 、三角形の内接円 この1点で交わった点 i を三角形の内心という。 内心 i を中心として、 半径 il の円が三角形の内接円である。 il＝im＝in il⊥bc 、 im⊥ac 、 in⊥ab

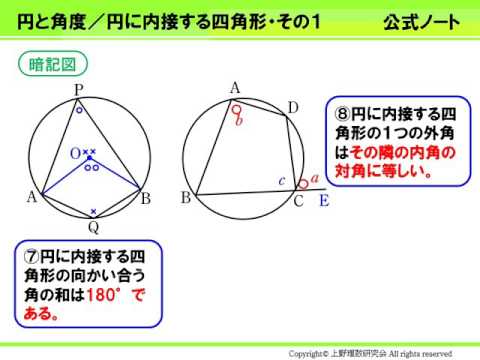
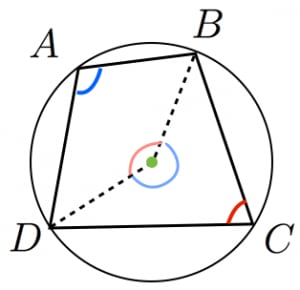
円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語

円と三角形 角度 中学から数学だいすき

Emathソースコード 円に内接する四角形と角度 数樂管理人のブログ

接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clear

角度 円と四角形 中学から数学だいすき

中学数学 円周角 中心角

内接円 内心

円に内接する四角形

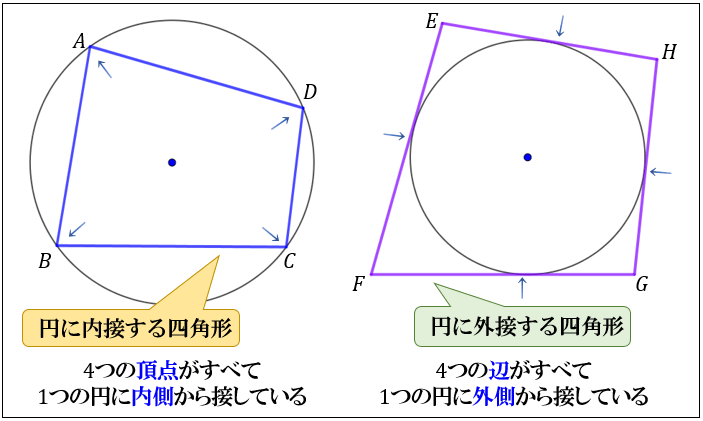
57 円に内接する三角形 と 円に内接する四角形 を比べる とちぎｅライブラリ

円と三角形 角度 中学から数学だいすき

Excel Vba 数学実験室 正三角形と内接する円の面積比

円に内接する三角形について 次の問題がわかりません 教えていただ 数学 教えて Goo

外接円 外心について

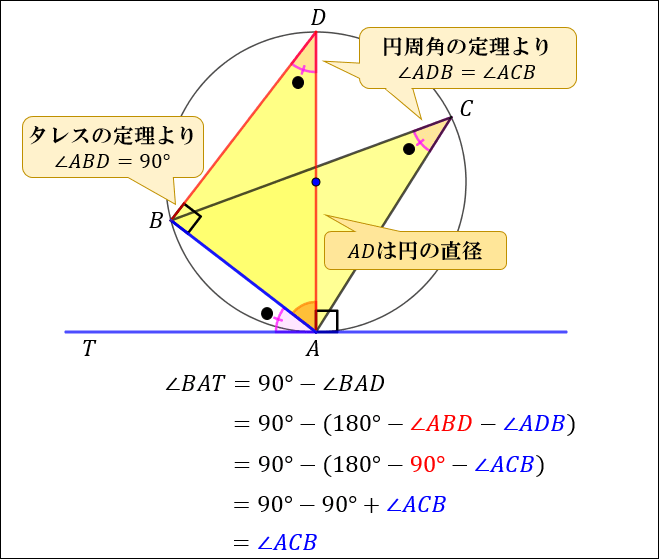
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

中3 数学 円に内接する四角形の問題です この問題がわからないので 教 数学 教えて Goo

円と角度04 内接四角形の性質 Youtube

内接円と角の２等分 中学数学の無料オンライン学習サイトchu Su

円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ

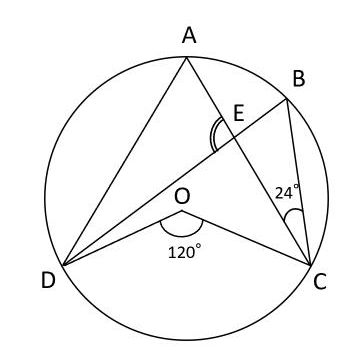
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

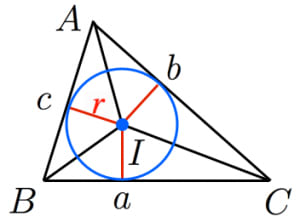
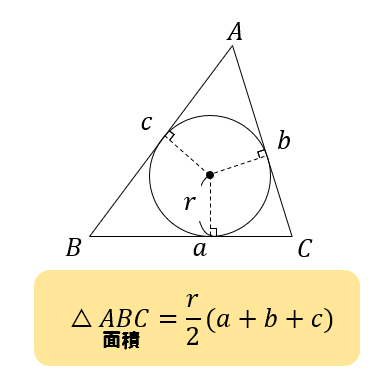
内接円の半径と三角形の面積 高校数学の美しい物語

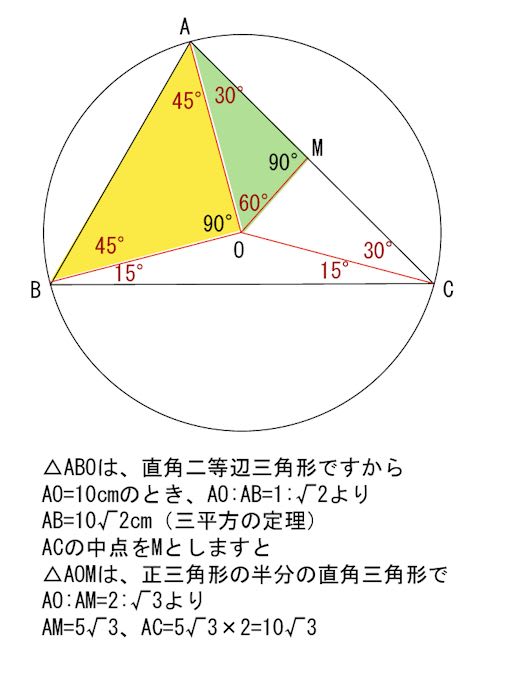
円に内接する 三角形の 問題 3 名寄 算数数学教室より

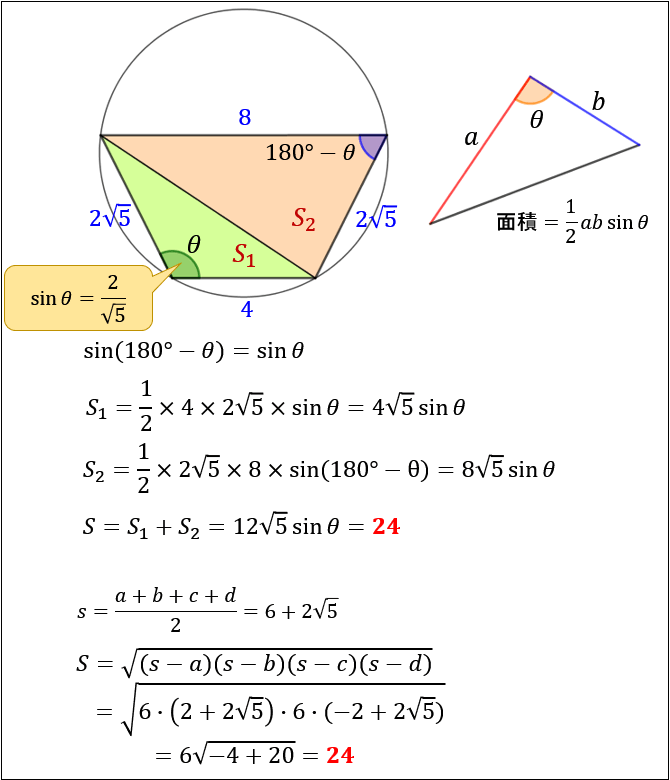
円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ

三角形の内接円 中学数学の無料オンライン学習サイトchu Su

円に内接する四角形の面積の求め方と定理の使い方

円に内接する三角形の解き方がわかりません っpreasehel Yahoo 知恵袋

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su

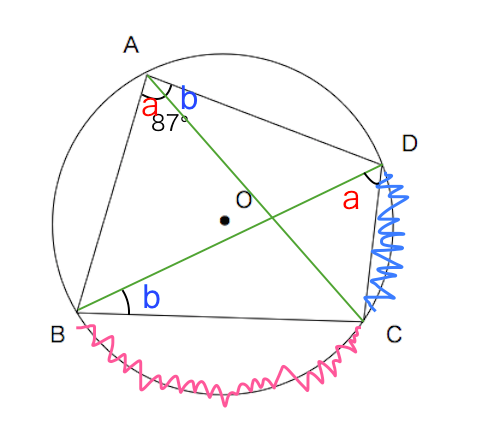
Aの角度を教えてください 円に内接する四角形の対角の和が180 よ Yahoo 知恵袋

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

円に内接する四角形 苦手な数学を簡単に

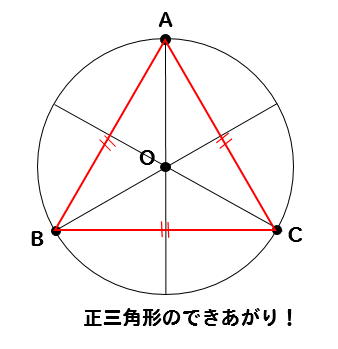
作図 円に内接する正三角形の作図方法とは 数スタ

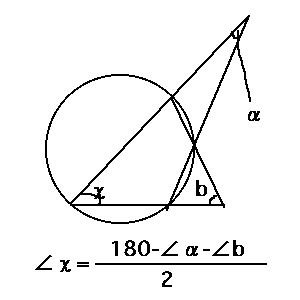
角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ

この２つの問題の角xの部分の解き方と答えを教えてください Clear

円に内接する三角形の角度xを求める問題がどうしてもわかりません Yahoo 知恵袋

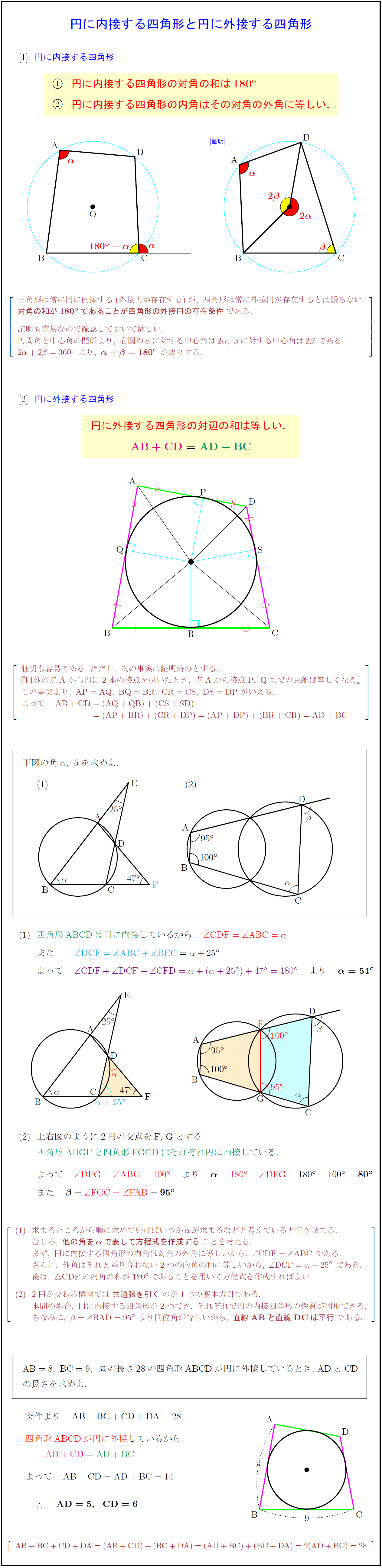
高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月

図形

円に内接する三角形の角度xを求める問題がどうしてもわかりません Yahoo 知恵袋

円に内接する四角形の性質 中学３年数学 Youtube

円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語

Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ

内接円 内心

作図 円に内接する正三角形の作図方法とは 数スタ

作図 三角形の内接円 外接円のかき方をポイント解説 数スタ

円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ

高校数学 数 ９６ 円に内接する四角形 Youtube

高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月

中学数学 円周角 中心角

円に内接する 三角形の 問題 4 名寄 算数数学教室より

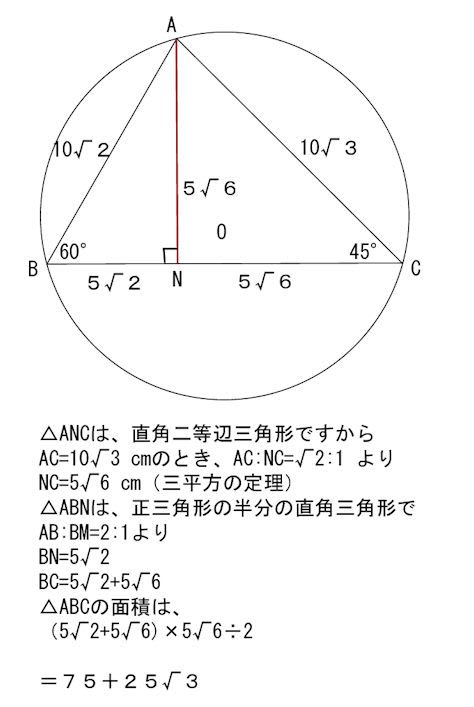
三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ

内接円 内心

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

中学数学 円周角 中心角

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

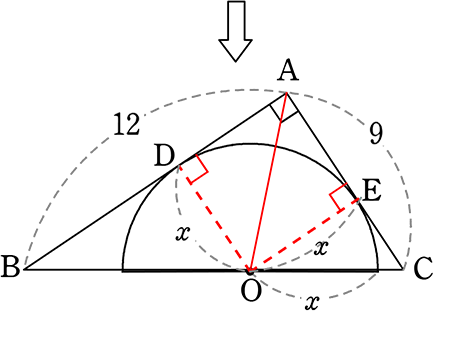
中学数学 円周角 中心角

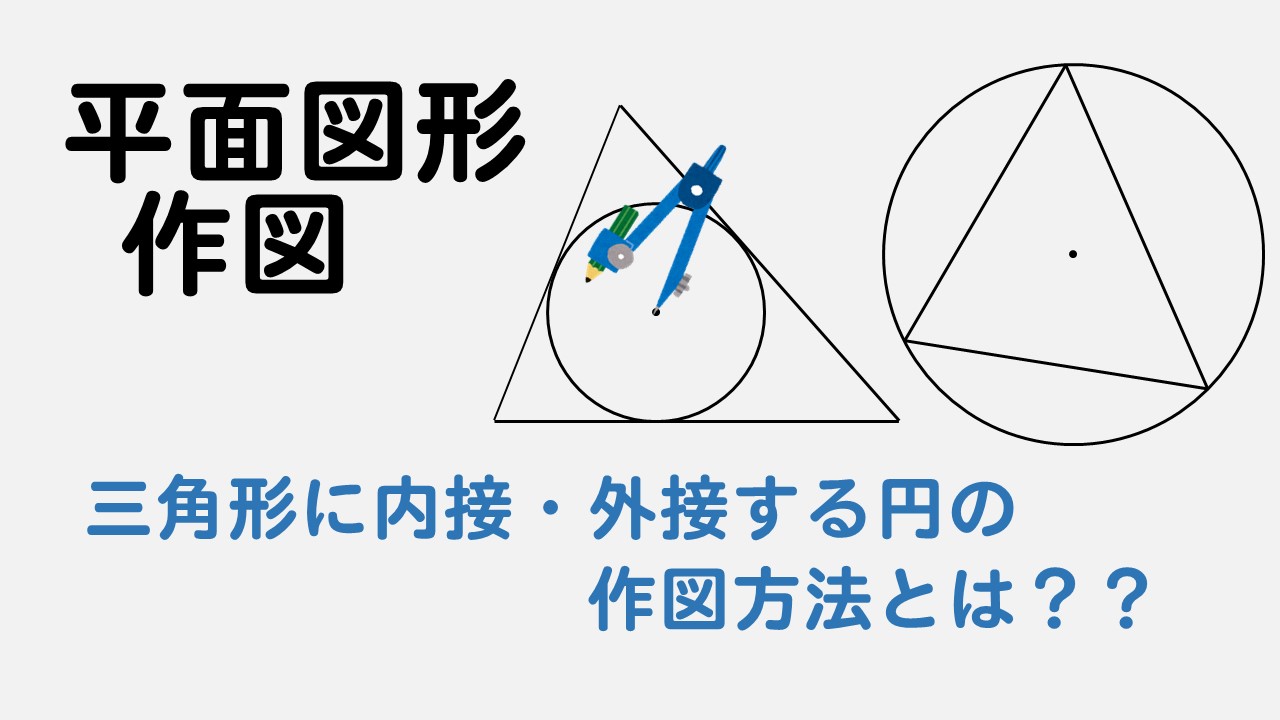
作図 三角形の内接円 外接円のかき方をポイント解説 数スタ

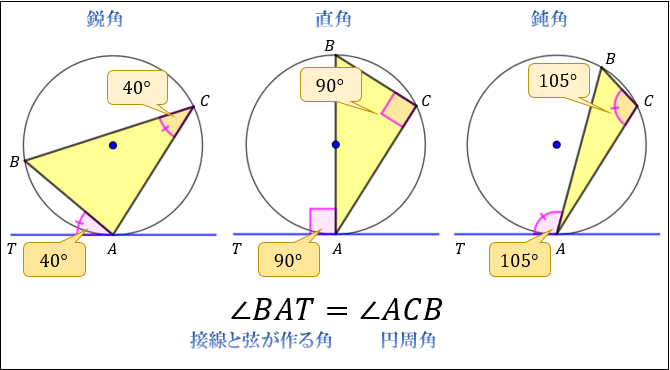
接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

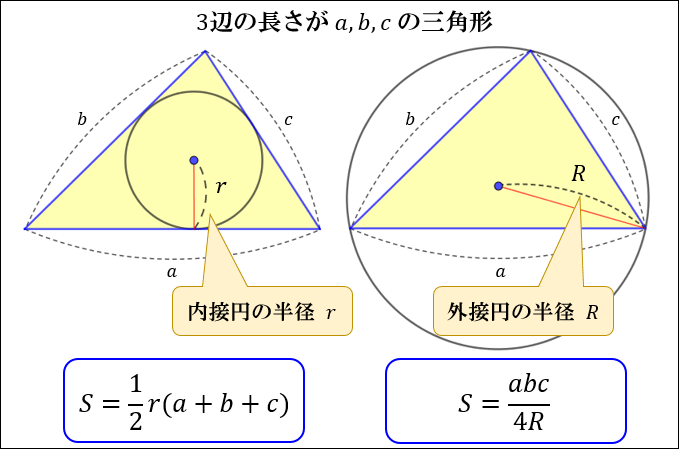
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

高校数学 円に内接する四角形の対角線の長さと面積 受験の月

円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

円の中からはみ出ている三角形の問題はどう解けばいいですか 角度x角度yを Yahoo 知恵袋

角度を求めて下さい 角度を求めて下さい 図のように 円に内接する 数学 教えて Goo

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

三角形の中に円 内接円 があるときの画像の8 内心の角度 は Yahoo 知恵袋

円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語

接線と円の関係 Jsciencer

円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

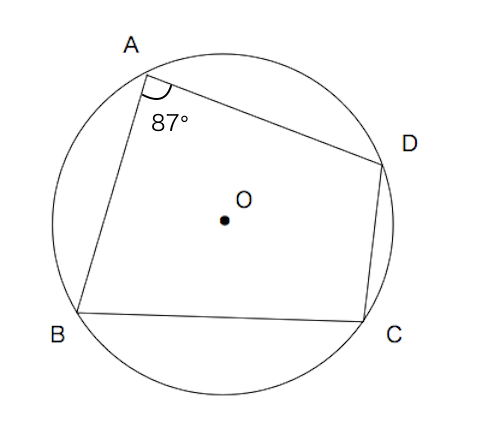
円に内接する四角形 苦手な数学を簡単に

三角形に内接する相似三角形 Geogebra

七五三 三角形から円に内接する四角形へ

Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ The 2nd

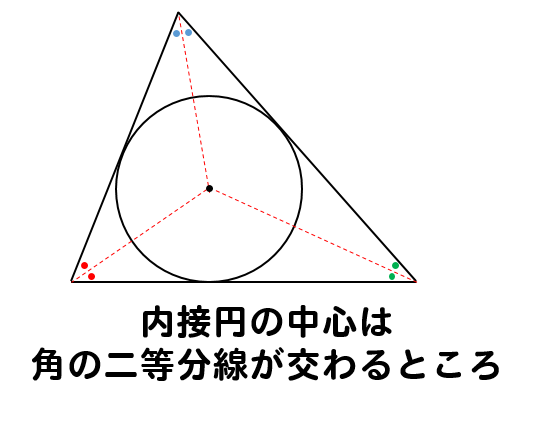
作図 三角形の内接円 外接円のかき方をポイント解説 数スタ

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

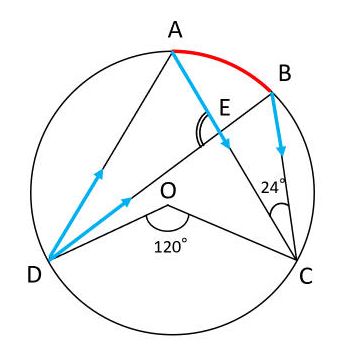
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

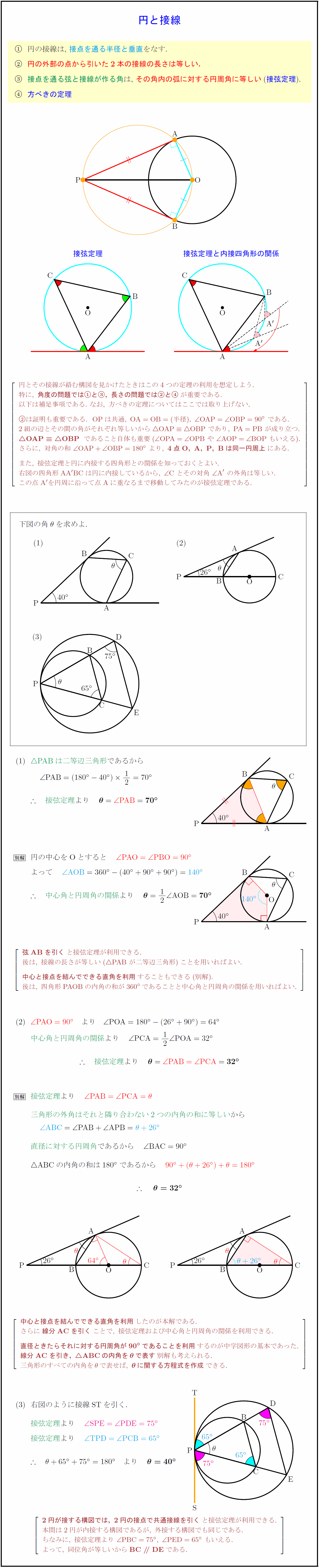
高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月

七五三 三角形から円に内接する四角形へ

円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

中3 円周角 円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 デジタル板書データ Youtube

七五三 三角形から円に内接する四角形へ

内接円 内心

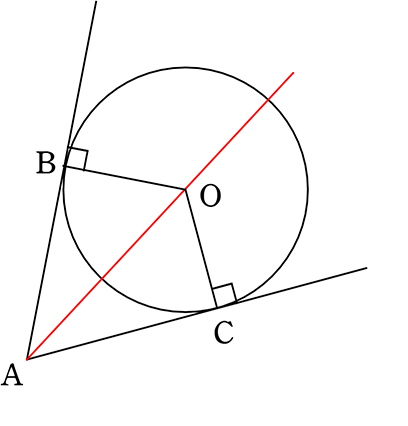
中学数学 円周角 中心角

中学数学 円周角 中心角

中学数学 円の中の三角形の角度の問題 Okwave

中学数学 円周角 中心角

Incoming Term: 円 内接 三角形 角度,